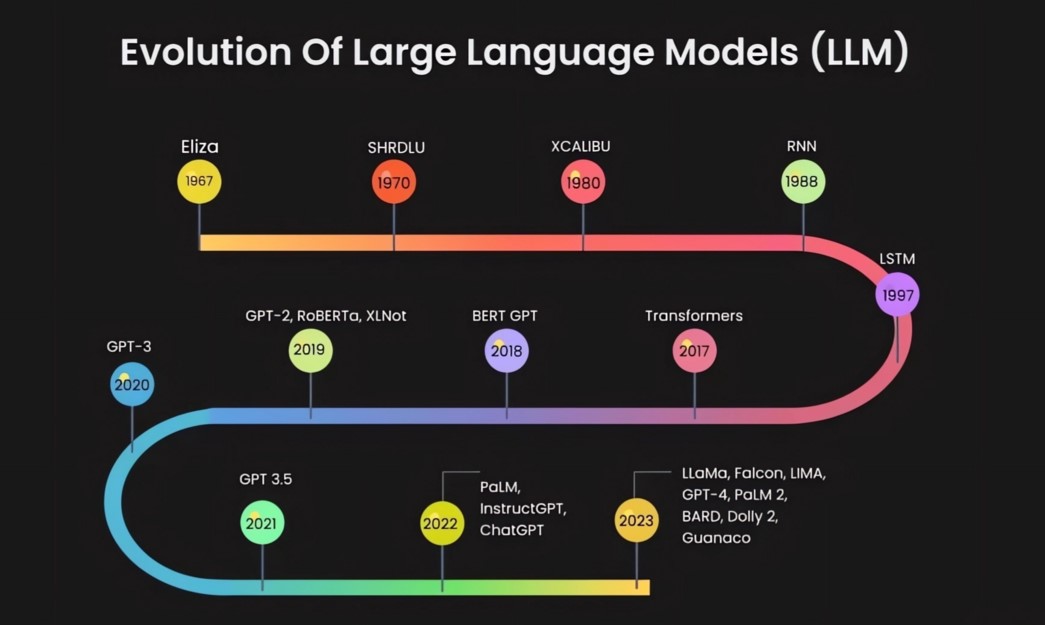
Kudos AI | Blog | The Evolution of Language Models: From N-grams to Transformers

The Evolution of Language Models: From N-grams to Transformers

Language models have undergone significant evolution over the decades, transforming from simple statistical approaches to complex deep learning architectures. This evolution reflects the broader advances in computational linguistics and artificial intelligence (AI), particularly in how machines understand and generate human language. This article will explore the major milestones in the evolution of language models, from the early days of N-grams to the transformative impact of Transformer models.

1. Early Language Models: The N-gram Approach

The earliest language models were based on N-grams, which are contiguous sequences of N items from a given text or speech. In the context of language models, these items are typically words or characters. The concept is straightforward: an N-gram model predicts the probability of a word based on the previous N-1 words. For example, a bigram model (N=2) predicts the next word based on the previous word, while a trigram model (N=3) predicts the next word based on the two preceding words.

N-gram models became popular in the 1950s and 1960s, particularly in the field of computational linguistics, as they offered a practical way to model the probability of sequences in language. One of the earliest applications of N-gram models was in the field of speech recognition, where they were used to predict the likelihood of word sequences based on previously observed patterns in large corpora of text or transcribed speech.

The mathematical foundation of N-gram models is rooted in probability theory, specifically in the Markov assumption, which posits that the probability of a word depends only on a fixed number of preceding words, regardless of the words that came before them. This assumption simplifies the modeling process but also introduces some limitations, as it fails to capture long-range dependencies in language.

Mathematically, the probability of a word sequence $ w_1, w_2, \ldots, w_n $ in an N-gram model is calculated as:

$$ P(w_1, w_2, \ldots, w_n) \approx \prod_{i=1}^{n} P(w_i|w_{i-N+1}, \ldots, w_{i-1}) $$

Where $ P(w_i|w_{i-N+1}, \ldots, w_{i-1}) $ is the conditional probability of word $ w_i $ given the preceding N-1 words. This conditional probability is typically estimated from a large corpus of text using maximum likelihood estimation (MLE) or smoothing techniques to handle the issue of unseen word sequences in the training data.

Despite their simplicity, N-gram models laid the groundwork for more advanced language modeling techniques by introducing the idea of capturing statistical patterns in language. However, they also suffer from several well-known limitations:

Data Sparsity: As the value of N increases, the number of possible N-grams grows exponentially, leading to many sequences with zero or very low probability due to insufficient training data. This issue is particularly problematic in languages with rich morphology or large vocabularies, where it becomes challenging to collect enough data to cover all possible N-grams.
Short Context Window: N-gram models can only consider a fixed number of preceding words, which limits their ability to capture long-range dependencies in text. For example, a trigram model cannot account for the influence of a word that appears four or five words earlier, even if that word is semantically important for understanding the current context.
Curse of Dimensionality: The dimensionality of the model increases with N, requiring more computational resources and data to achieve reasonable performance. As a result, practitioners often face a trade-off between the size of N and the practical limitations of computational power and data availability.

To mitigate some of these issues, researchers introduced various smoothing techniques, such as Laplace smoothing, Good-Turing discounting, and backoff models. These methods adjust the probability estimates for unseen N-grams, ensuring that the model can generalize better to new data. However, while these techniques improve the robustness of N-gram models, they do not fundamentally address the limitations of short context windows and the inability to capture long-range dependencies.

As a result, the need for more powerful language models became increasingly apparent, leading to the development of more sophisticated statistical methods that could better capture the complexities of human language.

2. Advancements in Statistical Language Models

To address the limitations of N-gram models, researchers developed more sophisticated statistical language models. These models leverage probabilistic methods to capture more complex dependencies between words, allowing for better generalization and performance.

One of the most significant advancements in this area was the introduction of Hidden Markov Models (HMMs). HMMs became widely used in the 1980s and 1990s, particularly in the field of speech recognition. They represent a major step forward in language modeling by allowing the modeling of sequential data with a probabilistic framework that considers both observed and hidden (latent) variables.

2.1 Hidden Markov Models (HMMs)

Hidden Markov Models (HMMs) are a class of statistical models that are particularly effective in tasks involving sequential data, such as speech recognition and part-of-speech tagging. An HMM consists of a set of hidden states, each associated with a probability distribution over possible output symbols (words, in the case of language models). The model transitions between these hidden states according to a set of transition probabilities, generating a sequence of observed words.

One of the key strengths of HMMs is their ability to model temporal dependencies in sequences by explicitly representing the state transitions over time. This makes them well-suited for tasks where the order of words or events is crucial, such as in language processing or time series analysis.

The key mathematical components of an HMM are:

Transition Probabilities ($ A $): The probability of transitioning from one hidden state to another. These probabilities are represented by a matrix where each entry $ A_{ij} $ represents the probability of moving from state $ i $ to state $ j $.
Emission Probabilities ($ B $): The probability of a particular word being generated from a given hidden state. This is represented by a matrix where each entry $ B_j(k) $ represents the probability of emitting observation $ k $ from state $ j $.
Initial State Distribution ($ \pi $): The probability distribution over the initial hidden states. This is a vector where each entry $ \pi_i $ represents the probability of the HMM starting in state $ i $.

The joint probability of a sequence of observed words $ O = (o_1, o_2, \ldots, o_T) $ and a sequence of hidden states $ S = (s_1, s_2, \ldots, s_T) $ in an HMM is given by:

$$ P(O, S) = \pi_{s_1} \cdot B_{s_1}(o_1) \cdot \prod_{t=2}^{T} A_{s_{t-1}, s_t} \cdot B_{s_t}(o_t) $$

Where:

$ \pi_{s_1} $ is the initial state probability for the first hidden state.
$ B_{s_1}(o_1) $ is the emission probability for the first observation given the first hidden state.
$ A_{s_{t-1}, s_t} $ is the transition probability from the previous hidden state to the current hidden state.
$ B_{s_t}(o_t) $ is the emission probability for the current observation given the current hidden state.

HMMs were a significant step forward in language modeling, but they still faced challenges in modeling long-range dependencies and handling large vocabularies. Additionally, HMMs assume that the probability of transitioning between states depends only on the current state, which can be limiting in cases where more complex dependencies exist between observations. To address these challenges, researchers explored alternative approaches that could model richer dependencies between words and capture more contextual information.

2.2 Conditional Random Fields (CRFs)

Conditional Random Fields (CRFs) are another type of statistical model used for structured prediction tasks, such as sequence labeling. Unlike HMMs, which model the joint probability of observed and hidden states, CRFs directly model the conditional probability of the output labels given the input sequence. This makes CRFs particularly effective for tasks where the goal is to predict a sequence of labels based on observed features, such as in part-of-speech tagging or named entity recognition.

CRFs were introduced in the early 2000s as a way to overcome some of the limitations of HMMs, particularly the assumption of independence between observations given the hidden state. In CRFs, the relationship between the input sequence and the output labels is modeled using a set of feature functions, which can capture a wide range of dependencies and interactions between the input and output variables.

The conditional probability of a label sequence $ Y = (y_1, y_2, \ldots, y_T) $ given an input sequence $ X = (x_1, x_2, \ldots, x_T) $ is defined as:

$$ P(Y|X) = \frac{1}{Z(X)} \exp\left( \sum_{t=1}^{T} \sum_{k} \lambda_k f_k(y_t, y_{t-1}, X, t) \right) $$

Where:

$ Z(X) $ is the normalization factor, ensuring that the probabilities sum to 1.
$ f_k(y_t, y_{t-1}, X, t) $ is a feature function that captures the relationship between the input and output at position $ t $. These feature functions can include both local features (e.g., the current word and its surrounding context) and global features (e.g., the overall structure of the sequence).
$ \lambda_k $ is a weight parameter learned during training, which determines the importance of each feature in the final prediction.

CRFs offer greater flexibility than HMMs, allowing for the incorporation of rich, overlapping features. They have been widely used in NLP tasks such as named entity recognition (NER), part-of-speech tagging, and shallow parsing, where they outperform HMMs by capturing more complex dependencies between labels. The ability of CRFs to model interactions between features and labels makes them particularly effective in scenarios where the output labels are not independent of each other, as is often the case in language processing tasks.

However, while CRFs represent an important advancement in statistical language modeling, they still have limitations. For instance, training CRFs can be computationally expensive, particularly for large datasets or complex feature sets. Additionally, like HMMs, CRFs are limited in their ability to model long-range dependencies, as they typically consider only a limited context window around each word in the sequence.

As the demand for more powerful language models continued to grow, researchers began to explore neural network-based approaches that could overcome these limitations and better capture the intricate patterns in natural language.

3. The Rise of Neural Language Models

The advent of deep learning brought about a paradigm shift in language modeling. Neural networks, with their ability to learn complex patterns from data, have revolutionized the field, leading to the development of neural language models that surpass the capabilities of traditional statistical models.

One of the earliest and most influential neural architectures for language modeling was the Recurrent Neural Network (RNN). RNNs are designed to handle sequential data by maintaining a hidden state that evolves over time, allowing them to capture temporal dependencies in sequences of arbitrary length. This makes RNNs particularly well-suited for tasks involving sequences, such as language modeling, machine translation, and speech recognition.

3.1 Recurrent Neural Networks (RNNs)

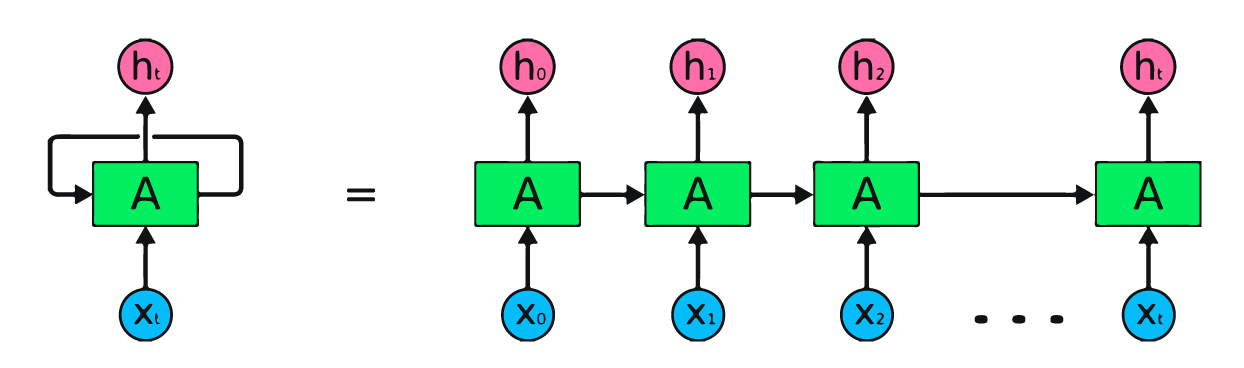
Recurrent Neural Networks (RNNs) are a class of neural networks designed to handle sequential data. Unlike feedforward networks, which process inputs independently, RNNs have a cyclic connection that allows information to persist across time steps. This cyclic structure enables RNNs to maintain a "memory" of previous inputs, making them well-suited for tasks where the order of inputs matters, such as language modeling.

The key idea behind RNNs is the concept of hidden states, which serve as a kind of dynamic memory that is updated at each time step based on the current input and the previous hidden state. This allows the network to retain information about past inputs and use it to inform future predictions.

In an RNN, the hidden state $ h_t $ at time step $ t $ is computed as:

$$ h_t = \tanh(W_{hx} x_t + W_{hh} h_{t-1} + b_h) $$

Where:

$ x_t $ is the input at time step $ t $.
$ h_{t-1} $ is the hidden state from the previous time step.
$ W_{hx} $ and $ W_{hh} $ are weight matrices that control the influence of the current input and the previous hidden state, respectively.
$ b_h $ is a bias term that allows the network to learn an offset for the hidden state.

The output at time step $ t $ is then computed as:

$$ y_t = W_{hy} h_t + b_y $$

Where:

$ W_{hy} $ is the output weight matrix that maps the hidden state to the output space.
$ b_y $ is a bias term that allows the network to learn an offset for the output.

RNNs can theoretically capture long-range dependencies in text, but in practice, they suffer from the problem of vanishing and exploding gradients, which makes it difficult to train them on long sequences. The vanishing gradient problem occurs when the gradients of the loss function with respect to the parameters become very small, leading to slow or stalled learning. The exploding gradient problem, on the other hand, occurs when the gradients become very large, leading to unstable updates and divergence during training.

These challenges led to the development of more advanced architectures, such as Long Short-Term Memory (LSTM) networks and Gated Recurrent Units (GRUs), which introduce mechanisms to better handle long-range dependencies and mitigate the issues of vanishing and exploding gradients.

3.2 Long Short-Term Memory (LSTM) Networks

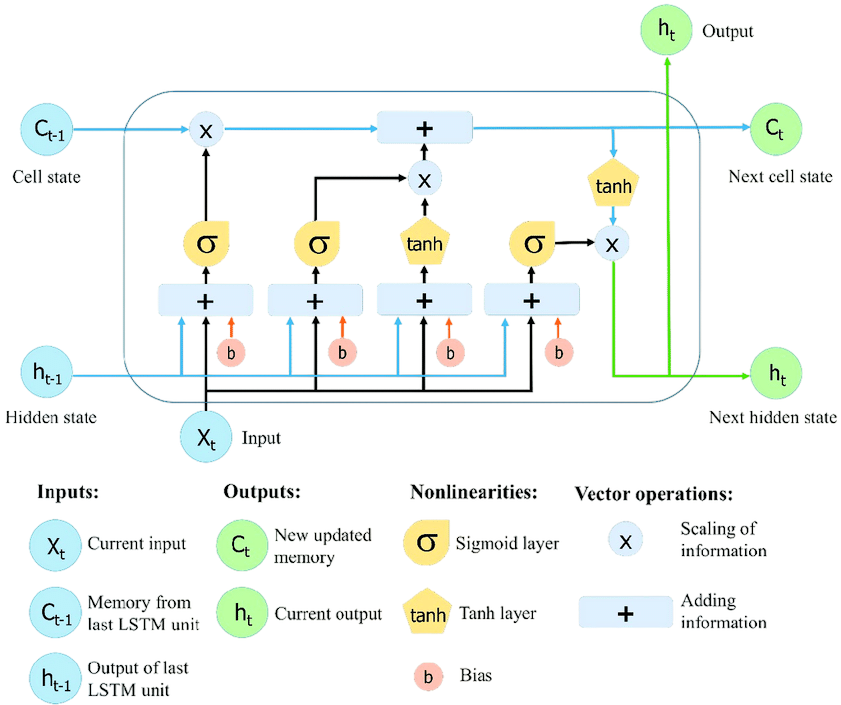
Long Short-Term Memory (LSTM) networks are a type of RNN specifically designed to address the vanishing gradient problem. They introduce a memory cell that can maintain information over long periods, along with gating mechanisms that control the flow of information into and out of the cell.

The key innovation of LSTMs is the use of gates—sigmoid neural networks that decide which information should be added to or removed from the memory cell. These gates allow the LSTM to selectively retain or discard information, enabling the network to capture long-range dependencies more effectively than traditional RNNs.

The key components of an LSTM cell include:

Forget Gate ($ f_t $): Determines which information to discard from the cell state. The forget gate outputs a value between 0 and 1 for each number in the cell state $ C_{t-1} $, where 1 represents "completely keep this" and 0 represents "completely forget this."
Input Gate ($ i_t $): Decides which information to update in the cell state. The input gate controls how much of the new information (i.e., the current input and the previous hidden state) will be used to update the cell state.
Cell State ($ C_t $): The internal memory of the cell that carries information across time steps. The cell state is updated by combining the information retained by the forget gate and the new information from the input gate.
Output Gate ($ o_t $): Controls the output of the cell, which will be used as the hidden state for the next time step. The output gate determines which parts of the cell state will be used to compute the hidden state.

The LSTM update equations are as follows:

$$ f_t = \sigma(W_f \cdot [h_{t-1}, x_t] + b_f) $$ $$ i_t = \sigma(W_i \cdot [h_{t-1}, x_t] + b_i) $$ $$ \tilde{C}_t = \tanh(W_C \cdot [h_{t-1}, x_t] + b_C) $$ $$ C_t = f_t \cdot C_{t-1} + i_t \cdot \tilde{C}_t $$ $$ o_t = \sigma(W_o \cdot [h_{t-1}, x_t] + b_o) $$ $$ h_t = o_t \cdot \tanh(C_t) $$

LSTM networks have become the go-to architecture for sequence modeling tasks where long-term dependencies are critical, such as machine translation, speech recognition, and text generation. Their ability to capture context over long sequences has led to significant improvements in the performance of language models on a wide range of NLP tasks.

3.3 Gated Recurrent Units (GRUs)

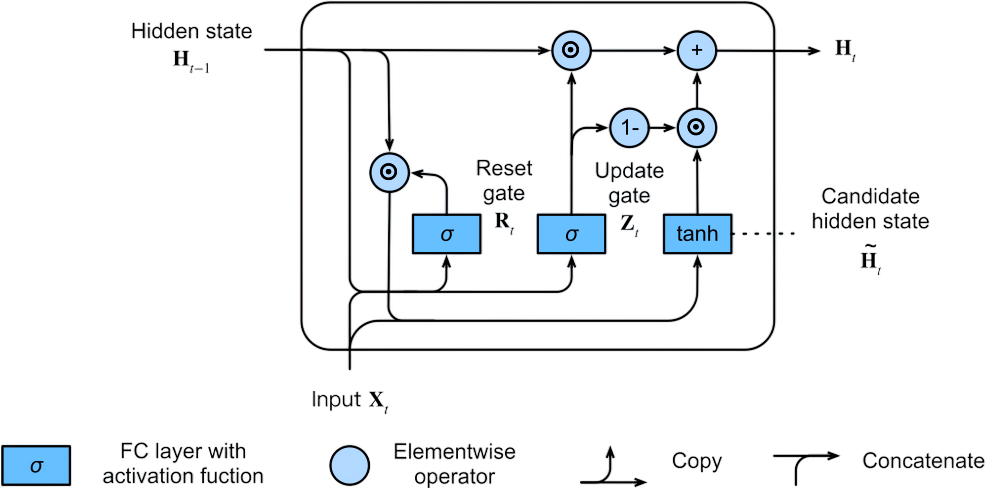
Gated Recurrent Units (GRUs) are a simplified variant of LSTM networks that combine the forget and input gates into a single update gate, making them computationally more efficient while retaining the ability to capture long-term dependencies.

The GRU architecture was introduced in 2014 as a way to simplify the LSTM model while preserving its key advantages. GRUs are similar to LSTMs in that they use gating mechanisms to control the flow of information, but they have fewer parameters, which makes them faster to train and more efficient in practice.

The GRU update equations are:

$$ z_t = \sigma(W_z \cdot [h_{t-1}, x_t] + b_z) $$ $$ r_t = \sigma(W_r \cdot [h_{t-1}, x_t] + b_r) $$ $$ \tilde{h}_t = \tanh(W_h \cdot [r_t \cdot h_{t-1}, x_t] + b_h) $$ $$ h_t = (1 - z_t) \cdot h_{t-1} + z_t \cdot \tilde{h}_t $$

Where:

$ z_t $ is the update gate, which controls the balance between retaining the previous hidden state $ h_{t-1} $ and updating it with the new candidate hidden state $ \tilde{h}_t $.
$ r_t $ is the reset gate, which controls how much of the previous hidden state $ h_{t-1} $ to forget when computing the new candidate hidden state $ \tilde{h}_t $.
$ \tilde{h}_t $ is the candidate hidden state, computed using the reset gate.

GRUs have gained popularity in applications where computational efficiency is essential, such as real-time language processing tasks. Despite their simpler structure, GRUs have been shown to perform competitively with LSTMs on many NLP tasks, making them a popular choice for researchers and practitioners alike.

While RNNs, LSTMs, and GRUs represent significant advancements in neural language modeling, they still have limitations, particularly when it comes to capturing global context and handling long-range dependencies in text. These challenges led to the development of the Transformer model, which has since become the dominant architecture in NLP.

4. The Transformer Revolution

The introduction of the Transformer model in 2017 marked a turning point in the field of NLP. Unlike RNNs, Transformers do not rely on sequential data processing, allowing them to process entire sequences in parallel. This fundamental shift enables Transformers to capture global dependencies in text more effectively and efficiently.

The Transformer architecture was first introduced in the paper "Attention is All You Need" by Vaswani et al. (2017). The key innovation of the Transformer is its use of self-attention mechanisms, which allow the model to weigh the importance of different words in a sequence when making predictions. This enables the Transformer to capture relationships between words regardless of their position in the sequence, making it particularly effective for tasks like machine translation, text summarization, and question answering.

4.1 Self-Attention Mechanism

At the core of the Transformer architecture is the self-attention mechanism, which allows the model to weigh the importance of different words in a sequence when making predictions. The self-attention mechanism computes a weighted sum of all words in the sequence, where the weights are determined by the relevance of each word to the current word.

The self-attention mechanism is defined as:

$$ \text{Attention}(Q, K, V) = \text{softmax}\left(\frac{QK^T}{\sqrt{d_k}}\right)V $$

Where:

$ Q $ is the query matrix, which represents the current word.
$ K $ is the key matrix, which represents the other words in the sequence.
$ V $ is the value matrix, which represents the word embeddings to be weighted and summed.
$ d_k $ is the dimensionality of the key vectors, used to scale the dot product of $ Q $ and $ K $ to stabilize training.

Self-attention enables the Transformer to capture dependencies between words regardless of their distance in the sequence, making it particularly effective for tasks like machine translation, text summarization, and question answering.

4.2 Multi-Head Attention

The Transformer extends the self-attention mechanism with multi-head attention, where multiple attention heads are used to focus on different parts of the sequence simultaneously. Each attention head performs self-attention independently, and their outputs are concatenated and linearly transformed to produce the final output.

The multi-head attention mechanism is defined as:

$$ \text{MultiHead}(Q, K, V) = \text{Concat}(\text{head}_1, \text{head}_2, \ldots, \text{head}_h)W^O $$ $$ \text{where head}_i = \text{Attention}(QW_i^Q, KW_i^K, VW_i^V) $$

This approach allows the model to capture different aspects of the input sequence, enhancing its ability to understand and generate complex language structures. By using multiple attention heads, the Transformer can focus on different relationships between words, capturing both local and global dependencies in the sequence.

Multi-head attention is a key component of the Transformer's success, as it allows the model to process information in parallel and capture a richer set of relationships between words in the sequence. This capability has made the Transformer the architecture of choice for many state-of-the-art language models.

4.3 Transformer Applications: GPT, BERT, and Beyond

The Transformer architecture has become the foundation for many state-of-the-art language models, including GPT, BERT, and T5. These models have achieved unprecedented performance across a wide range of NLP tasks, from language generation to sentiment analysis.

GPT (Generative Pre-trained Transformer): GPT models are autoregressive language models that generate text by predicting the next word in a sequence. GPT-3, the latest version, has 175 billion parameters, making it one of the largest and most powerful language models to date. GPT models are trained on large corpora of text data, allowing them to generate human-like text across a wide range of topics and styles. GPT-3 has been used in applications ranging from chatbots to content creation, and it represents a significant step forward in the development of general-purpose language models.
BERT (Bidirectional Encoder Representations from Transformers): BERT is a bidirectional language model that captures context from both directions in a text sequence. This bidirectional approach allows BERT to achieve state-of-the-art performance on a variety of NLP tasks, including question answering, text classification, and named entity recognition. BERT is pre-trained on a large corpus of text using a masked language modeling objective, where some words in the input are randomly masked, and the model is trained to predict the masked words. This pre-training allows BERT to learn rich contextual representations of words, which can be fine-tuned for specific tasks.
T5 (Text-To-Text Transfer Transformer): T5 is a model that treats all NLP tasks as text-to-text problems, allowing it to excel at tasks such as translation, summarization, and question answering. T5 is pre-trained on a large corpus of text using a denoising objective, where some words or phrases in the input are corrupted, and the model is trained to generate the correct text. This pre-training allows T5 to learn flexible and robust representations of text, which can be fine-tuned for a wide range of NLP tasks. T5's unified text-to-text framework has made it a popular choice for many NLP applications, as it simplifies the task of fine-tuning the model for different tasks.

The success of GPT, BERT, and T5 has led to the widespread adoption of the Transformer architecture in both academia and industry. These models have set new benchmarks for performance on many NLP tasks, and they have inspired the development of even larger and more powerful language models.

However, the increasing size and complexity of these models also raise challenges related to computational efficiency, interpretability, and ethical considerations. As the field continues to advance, researchers are exploring ways to address these challenges while further improving the capabilities of language models.

5. The Future of Language Models

The evolution of language models from N-grams to Transformers represents a profound shift in how machines process and generate human language. As research continues, we can expect even more sophisticated models that push the boundaries of what is possible in NLP.

One promising direction is the development of models that can better understand and generate human language in a more context-aware and nuanced manner. This includes models that can handle multimodal data (e.g., combining text with images or audio) and those that can engage in more natural, human-like conversations. Multimodal models, such as those that combine text with images or audio, have the potential to create richer and more interactive AI systems, capable of understanding and generating content across different media types.

Another important area of research is the development of models that are more efficient and scalable. While models like GPT-3 are incredibly powerful, they are also computationally expensive and require vast amounts of data and processing power to train. Future models may achieve similar or superior performance with fewer parameters and more efficient training algorithms. Techniques such as model compression, pruning, and knowledge distillation are being explored to reduce the size and complexity of language models without sacrificing performance.

In addition to improving efficiency, there is a growing interest in making language models more interpretable and explainable. As language models are increasingly used in high-stakes applications, such as healthcare, finance, and legal decision-making, it is crucial to understand how these models arrive at their predictions. Researchers are developing methods for visualizing and interpreting the internal workings of language models, such as attention maps and feature attribution methods, which help users and developers understand which parts of the input data are most influential in the model's decision-making process. This transparency is critical for building trust in AI systems, particularly in domains where the consequences of incorrect predictions can be severe.