The Transformer Architecture

The Transformer Architecture: Revolutionizing Natural Language Processing

The field of Natural Language Processing (NLP) has undergone a series of paradigm shifts, with the Transformer architecture standing out as a groundbreaking innovation. Introduced by Vaswani et al. in the seminal paper "Attention is All You Need" (2017), the Transformer has rapidly become the de facto standard for NLP tasks, replacing traditional models like Recurrent Neural Networks (RNNs) and Convolutional Neural Networks (CNNs). This article delves into the intricacies of the Transformer architecture, exploring how it has revolutionized NLP, supported by mathematical formulations and Python code snippets.

1. The Need for a New Architecture

Before the advent of the Transformer, NLP models primarily relied on RNNs and CNNs to process sequences of text. RNNs, with their ability to maintain hidden states, were particularly adept at handling sequential data, such as time series or text. However, RNNs suffered from limitations, most notably the vanishing gradient problem, which made it difficult for them to learn long-range dependencies in text.

1.1 The Vanishing Gradient Problem in RNNs

The vanishing gradient problem in RNNs occurs when gradients used for updating the network's weights become very small during backpropagation. This issue arises due to the multiplicative nature of gradient updates in RNNs, where the gradient can shrink exponentially as it is propagated backward through time.

The following Python code demonstrates a simple RNN step, where the hidden state \( h_t \) is updated based on the previous hidden state \( h_{t-1} \) and the current input \( x_t \). The vanishing gradient problem can manifest during backpropagation through these repeated steps. 


import numpy as np

def sigmoid(x):
    return 1 / (1 + np.exp(-x))

def rnn_step(x, h_prev, W_h, W_x, b_h):
    return sigmoid(np.dot(W_h, h_prev) + np.dot(W_x, x) + b_h)

Mathematically, if we consider a simple RNN with a hidden state \( h_t \) at time step \( t \), the update rule is given by:

$$ h_t = \sigma(W_h \cdot h_{t-1} + W_x \cdot x_t + b_h) $$

During backpropagation, the gradient of the loss with respect to the hidden state at time step \( t \) is computed as:

$$ \frac{\partial L}{\partial h_t} = \frac{\partial L}{\partial h_{t+1}} \cdot \frac{\partial h_{t+1}}{\partial h_t} $$

To mitigate the vanishing gradient problem, researchers developed more sophisticated variants of RNNs, such as Long Short-Term Memory (LSTM) networks and Gated Recurrent Units (GRUs).

1.2 CNNs and Their Limitations in NLP

Convolutional Neural Networks (CNNs) were adapted for NLP to capture local patterns, such as n-grams, across the input sequence. However, they struggle to model long-range dependencies because they rely on a fixed receptive field.

Below is a simple implementation of a CNN in PyTorch, where the model applies convolutional layers followed by a fully connected layer. While effective for capturing local features, CNNs struggle with long-range dependencies because each convolution operation only considers a local region of the input. 


import torch
import torch.nn as nn

class SimpleCNN(nn.Module):
    def __init__(self):
        super(SimpleCNN, self).__init__()
        self.conv1 = nn.Conv2d(in_channels=1, out_channels=32, kernel_size=3)
        self.fc1 = nn.Linear(32 * 6 * 6, 128)

    def forward(self, x):
        x = torch.relu(self.conv1(x))
        x = x.view(-1, 32 * 6 * 6)
        x = torch.relu(self.fc1(x))
        return x

1.3 The Quest for Better Contextual Understanding

Both RNNs and CNNs have inherent limitations in capturing global context and long-range dependencies in text. The quest for better contextual understanding in NLP led researchers to explore alternative architectures, resulting in the development of the Transformer architecture.

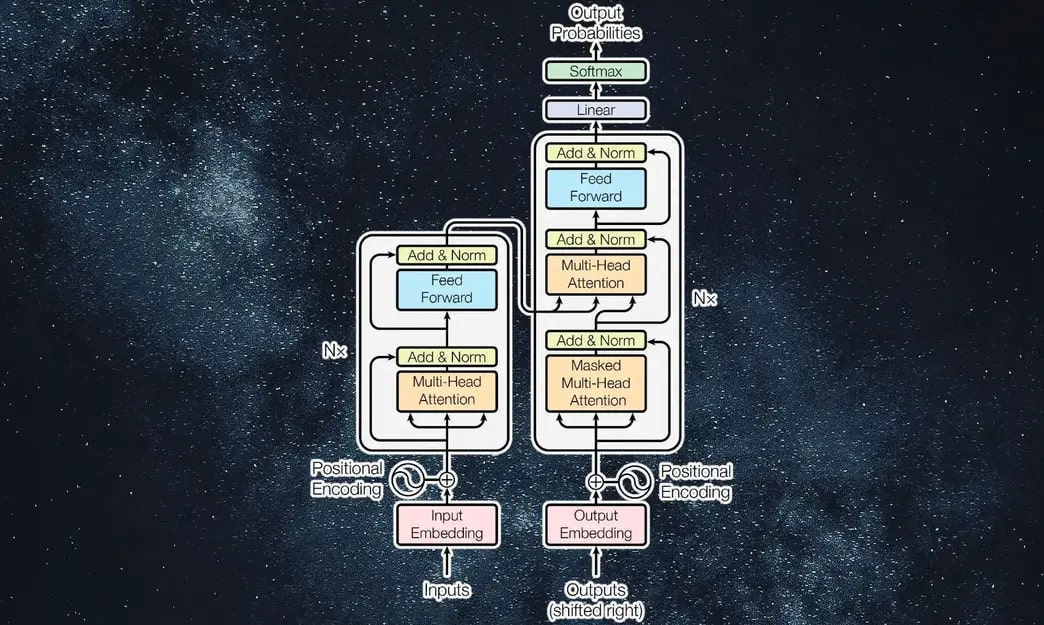
2. The Transformer Architecture

The Transformer architecture was introduced in the groundbreaking paper "Attention is All You Need" by Vaswani et al. (2017). It fundamentally changed the way we approach NLP tasks by eliminating the need for recurrent connections and relying entirely on attention mechanisms.

2.1 Self-Attention Mechanism

At the heart of the Transformer architecture is the self-attention mechanism, which allows the model to weigh the importance of different words in a sequence when making predictions. Self-attention computes a weighted sum of all words in the sequence.

The Python code snippet below implements a simplified version of the self-attention mechanism: 


import numpy as np

def scaled_dot_product_attention(Q, K, V):
    d_k = Q.shape[-1]
    scores = np.dot(Q, K.T) / np.sqrt(d_k)
    weights = softmax(scores, axis=-1)
    return np.dot(weights, V)

Mathematically, the self-attention mechanism is represented as:

$$ \text{Attention}(Q, K, V) = \text{softmax}\left(\frac{QK^T}{\sqrt{d_k}}\right)V $$

This self-attention mechanism allows the Transformer to capture dependencies between words regardless of their distance in the sequence, making it particularly effective for tasks like machine translation.


2.2 Multi-Head Attention

To capture different aspects of the input sequence, the Transformer employs a multi-head attention mechanism, where multiple attention heads are used to focus on different parts of the sequence simultaneously. Each attention head performs self-attention independently, and their outputs are concatenated and linearly transformed to produce the final output.

Below is an example implementation of a multi-head attention mechanism in PyTorch. The model splits the input into multiple heads, applies self-attention to each head independently, and then concatenates the results: 


import torch
import torch.nn as nn

class MultiHeadAttention(nn.Module):
    def __init__(self, d_model, num_heads):
        super(MultiHeadAttention, self).__init__()
        self.num_heads = num_heads
        self.d_model = d_model

        self.query = nn.Linear(d_model, d_model)
        self.key = nn.Linear(d_model, d_model)
        self.value = nn.Linear(d_model, d_model)
        self.out = nn.Linear(d_model, d_model)

    def forward(self, Q, K, V):
        batch_size = Q.size(0)

        # Linear layers
        Q = self.query(Q)
        K = self.key(K)
        V = self.value(V)

        # Split into num_heads
        Q = Q.view(batch_size, -1, self.num_heads, self.d_model // self.num_heads).transpose(1, 2)
        K = K.view(batch_size, -1, self.num_heads, self.d_model // self.num_heads).transpose(1, 2)
        V = V.view(batch_size, -1, self.num_heads, self.d_model // self.num_heads).transpose(1, 2)

        # Scaled dot-product attention
        attn_output, _ = scaled_dot_product_attention(Q, K, V)

        # Concatenate heads
        attn_output = attn_output.transpose(1, 2).contiguous().view(batch_size, -1, self.d_model)

        return self.out(attn_output)

By using multiple attention heads, the Transformer can capture a richer set of relationships between words, enhancing its ability to understand and generate complex language structures.

2.3 Positional Encoding

Since the Transformer processes the entire sequence in parallel, it lacks an inherent notion of word order. To address this, the Transformer introduces positional encodings, which are added to the input embeddings to provide information about the position of each word in the sequence.

The following Python code demonstrates how to calculate positional encodings for a sequence. These encodings use sine and cosine functions of different frequencies to ensure that each position has a unique representation: 


import numpy as np

def get_positional_encoding(seq_len, d_model):
    pos_encoding = np.zeros((seq_len, d_model))
    for pos in range(seq_len):
        for i in range(0, d_model, 2):
            pos_encoding[pos, i] = np.sin(pos / (10000 ** ((2 * i)/d_model)))
            pos_encoding[pos, i + 1] = np.cos(pos / (10000 ** ((2 * i)/d_model)))
    return pos_encoding

Mathematically, the positional encoding is given by:

$$ PE_{(pos, 2i)} = \sin\left(\frac{pos}{10000^{\frac{2i}{d}}}\right) $$ $$ PE_{(pos, 2i+1)} = \cos\left(\frac{pos}{10000^{\frac{2i}{d}}}\right) $$

The introduction of positional encodings ensures that the Transformer model can still leverage the sequence order, which is crucial for tasks like language modeling and translation.

2.4 Feed-Forward Neural Networks

Each layer in the Transformer consists of a multi-head attention mechanism followed by a feed-forward neural network (FFNN). The FFNN is applied independently to each position in the sequence, and it consists of two linear transformations with a ReLU activation in between.

The following code snippet shows a simple implementation of a feed-forward network used within a Transformer layer. It consists of two linear transformations with a ReLU activation in between: 


import torch.nn as nn

class FeedForwardNN(nn.Module):
    def __init__(self, d_model, d_ff):
        super(FeedForwardNN, self).__init__()
        self.fc1 = nn.Linear(d_model, d_ff)
        self.fc2 = nn.Linear(d_ff, d_model)

    def forward(self, x):
        return self.fc2(torch.relu(self.fc1(x)))

The mathematical representation of this feed-forward network is:

$$ FFN(x) = \text{ReLU}(xW_1 + b_1)W_2 + b_2 $$

The combination of multi-head attention and feed-forward networks in each layer of the Transformer enables the model to capture a wide range of dependencies in the input sequence, making it highly effective for various NLP tasks.

3. Transformer Applications in NLP

3.1 GPT: Generative Pre-trained Transformer

GPT models are autoregressive language models that generate text by predicting the next word in a sequence. GPT-3, the latest version, has 175 billion parameters, making it one of the largest and most powerful language models to date.

Below is a Python code snippet using the Hugging Face Transformers library to load a GPT-2 model and generate text. This illustrates how GPT models can be applied to real-world NLP tasks: 


from transformers import GPT2Tokenizer, GPT2LMHeadModel

# Load pre-trained model and tokenizer
tokenizer = GPT2Tokenizer.from_pretrained('gpt2')
model = GPT2LMHeadModel.from_pretrained('gpt2')

# Encode input text
input_ids = tokenizer.encode("The Transformer architecture", return_tensors='pt')

# Generate text
output = model.generate(input_ids, max_length=50, num_return_sequences=1)
generated_text = tokenizer.decode(output[0], skip_special_tokens=True)

print(generated_text)

One of the key innovations in the GPT series is the use of unsupervised pre-training followed by supervised fine-tuning.

3.2 BERT: Bidirectional Encoder Representations from Transformers

BERT is a bidirectional language model that captures context from both directions in a text sequence. This bidirectional approach allows BERT to achieve state-of-the-art performance on a variety of NLP tasks, including question answering, text classification, and named entity recognition.

The following code snippet demonstrates how to load a pre-trained BERT model and use it for sequence classification tasks: 


from transformers import BertTokenizer, BertForSequenceClassification

# Load pre-trained model and tokenizer
tokenizer = BertTokenizer.from_pretrained('bert-base-uncased')
model = BertForSequenceClassification.from_pretrained('bert-base-uncased')

# Encode input text
input_ids = tokenizer.encode("The Transformer architecture", return_tensors='pt')

# Get predictions
outputs = model(input_ids)
predictions = torch.argmax(outputs.logits, dim=-1)

print(predictions)

3.3 T5: Text-To-Text Transfer Transformer

T5 is a model that treats all NLP tasks as text-to-text problems, allowing it to excel at tasks such as translation, summarization, and question answering.

The Python code snippet below shows how to use the T5 model for translation tasks: 


from transformers import T5Tokenizer, T5ForConditionalGeneration

# Load pre-trained model and tokenizer
tokenizer = T5Tokenizer.from_pretrained('t5-small')
model = T5ForConditionalGeneration.from_pretrained('t5-small')

# Encode input text
input_text = "translate English to French: The Transformer architecture is revolutionary."
input_ids = tokenizer.encode(input_text, return_tensors='pt')

# Generate text
output = model.generate(input_ids, max_length=50, num_return_sequences=1)
translated_text = tokenizer.decode(output[0], skip_special_tokens=True)

print(translated_text)

4. The Future of Transformer Models

The Transformer architecture has set new benchmarks for NLP, but there is still room for improvement. Researchers are exploring ways to make Transformer models more efficient, interpretable, and capable of handling more complex tasks.

As language models are increasingly used in high-stakes applications, such as healthcare, finance, and legal decision-making, it is crucial to understand how these models arrive at their predictions.

4.1 Efficiency and Scalability

Researchers are exploring various techniques to address these challenges, including sparse attention mechanisms, which reduce the computational cost of self-attention by focusing on a subset of the input sequence.

4.2 Interpretability and Explainability

Attention maps, which visualize the weights assigned to different words in a sequence by the self-attention mechanism, are a common tool for interpreting Transformer models.

4.3 Ethical Considerations

The increasing size and complexity of language models raise important ethical considerations, particularly related to bias, privacy, and the potential misuse of AI. Researchers are actively working on methods to detect, quantify, and mitigate bias in language models.

5. Conclusion

The Transformer architecture has revolutionized the field of Natural Language Processing, providing a powerful and flexible framework for a wide range of NLP tasks. With its self-attention mechanism, multi-head attention, and ability to process sequences in parallel, the Transformer has overcome many of the limitations of previous architectures, such as RNNs and CNNs.

Looking forward, the future of Transformer models is likely to be characterized by increased efficiency, greater interpretability, and a stronger focus on ethical considerations.